自然语言处理之LDA II-Variational EM实现

发布于   |   分类于   |     |   阅读次数

上一篇 自然语言处理之LDA 使用Gibbs Sampling实现了LDA，本文使用Variational EM实现LDA。

LDA的概率图模型

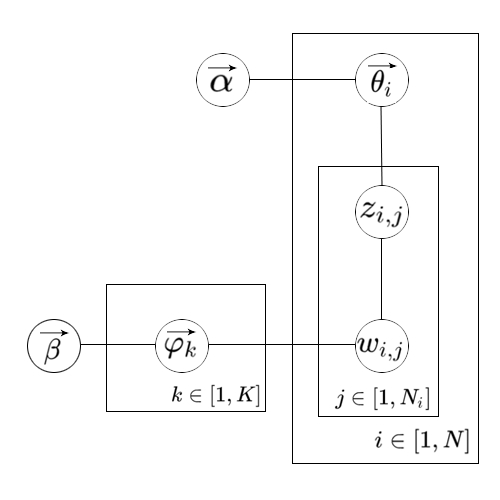
graphical-model
符号解释如下：

符号 描述
$N$ 文档总数
$N_i$ 第i篇文档单词数
$K$ topic总数
$M$ 词表长度
$\vec{\alpha}$ document-topic分布的超参数，是一个K维向量
$\vec{\beta}$ topic-word分布的超参数，是一个M维向量
$\vec{\theta_i}$ $p(z{\vert}d=i)$组成的K维向量，其中$z\in[1,K]$
$\vec{\varphi_k}$ $p(w{\vert}z=k)$组成的M维向量，其中$w\in[1,M]$
$z_{i,j}$ 第i篇文档的第j个单词的topic编号
$w_{i,j}$ 第i篇文档的第j个单词在词表中的编号

文档生成过程

LDA认为数据的生成过程如下图。在具体的实现中，会省略掉某些不重要的过程。比如文档长度$N_i$服从泊松分布的过程，在Gibbs Sampling以及本文Variational EM两种实现中都省略了。
此外，在本文Variational EM的实现中还将省略 ${\varphi_k}$ 的 $\beta$ 先验。
generate-process
那么先回忆一下，在PLSA的实现中使用到了EM算法，在随机的为模型的参数赋值之后就可以在E-Step计算出隐变量的后验概率，从而可以在M-Step优化模型参数，并不断迭代。
因此我们此时也应该尝试推出隐变量的后验概率的计算公式。
根据图模型，可以得到对于一篇文档来说隐变量的后验概率为：
$$
p(\vec{\theta}, \vec{z}|\vec{w},\vec{\alpha},\vec{\varphi})=\frac{p(\vec{\theta}, \vec{z},\vec{w}|\vec{\alpha},\vec{\varphi})}{p(\vec{w}|\vec{\alpha},\vec{\varphi})}
$$
其中分母部分通过引入模型参数可以表示为：
$$
\begin {aligned}
p(\vec{w}|\vec{\alpha},\vec{\varphi}) &={\int}p(\vec{\theta}|\vec{\alpha})(\prod^{N_i}_{n=1}\sum^{K}_{k=1}p(z_n=k|\vec{\theta})p(w_n|z_n=k))d\vec{\theta} \\
&={\int}p(\vec{\theta}|\vec{\alpha})(\prod^{N_i}_{n=1}\sum^{K}_{k=1}\prod^M_{j=1}(\theta_k\varphi_{kj})^{w_n^{j}})d\vec{\theta}
\end {aligned}
$$
这里出现了一个新的符号 $w_n^{j}$, 若该篇文档的第 $n$ 个词在词表中的编号为 $j$,则 $w_n^{j}=1$，否则$w_n^{j}=0$。
可以看到 $\theta$ 和 $\varphi$ 以乘积的形式结合在了隐变量的求和之中，因此无法直接根据上式计算出隐变量的后验概率。
因此我们在E-Step使用变分推断(Variational Inference)得到隐变量后验概率的近似值。
在介绍变分推断之前，先介绍一下在变分推断中要用到的Dirichlet分布的一些性质。

Dirichlet distribution

这里介绍Dirichlet分布的形式以及期望的计算公式。若 $\theta{\sim}Dirichlet(\alpha)$,则有：

$$
\begin {aligned}
p(\theta|\alpha) &=\frac{\Gamma(\sum^{K}_{i=1}\alpha_i)}{\sum^{K}_{i=1}\Gamma(\alpha_i)}\prod^{K}_{i=1}{\theta_i}^{\alpha_i-1} \\
&=exp((\sum^{K}_{i=1}(\alpha_i-1)log\theta_i)+log\Gamma(\sum^{K}_{i=1}\alpha_i)-\sum^{K}_{i=1}log\Gamma(\alpha_i))
\end {aligned}
$$

第二行将dirichlet分布化为了指数分布族的一般形式，可以得到:
sufficient statistics : $log\theta_i$
log normalizer : $\sum^{K}_{i=1}log\Gamma(\alpha_i)-log\Gamma(\sum^{K}_{i=1}\alpha_i)$
因此可以计算 $log\theta_i$的期望是：

$$
\begin {aligned}
E(log\theta_i) &=(\sum^{K}_{i=1}log\Gamma(\alpha_i)-log\Gamma(\sum^{K}_{i=1}\alpha_i))’ \\
&=\psi(\alpha_i)-\psi(\sum^{K}_{j=1}\alpha_j)
\end {aligned}
$$

这里的 $\Gamma$表示gamma函数; $\psi$ 表示digamma函数，是log Gamma函数的一阶导函数。

Variational Inference

变分推断的基本思想

变分推断要做的就是用分布q来近似隐变量的后验概率的分布。定义变分推断图模型如下。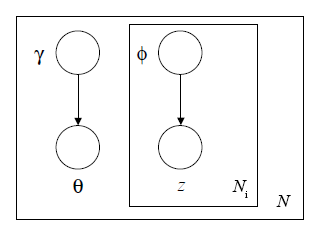
inference-graphical-model

根据图模型，可以得到对于隐变量的变分分布：
$$
q(\theta,z|\gamma,\phi)=q(\theta|\gamma)\prod^{N_i}_{n=1}q(z_n|\phi_n)
$$
那么如何来衡量这两个分布的差异性呢？我们使用KL散度（Kullback–Leibler divergence）,KL散度始终大于等于0，当且仅当两个分布相同时KL散度等于0。
我们的目标是找到参数 $\gamma$ 和 $\phi$ 使得KL散度越小越好。
即求解如下的优化问题：
$$
(\gamma^{\ast},\phi^{\ast})={arg}min_{\gamma,\phi}KL(q(\theta,z|\gamma,\phi)||p(\theta, z|w,\alpha,\varphi))
$$

那么我们来计算KL散度。
$$
\begin {aligned}
KL(q(\theta,z|\gamma,\phi)||p(\theta, z|w,\alpha,\varphi)) &=E_q(log\frac{q(\theta,z|\gamma,\phi)}{p(\theta, z|w,\alpha,\varphi)}) \\
&=E_q[log(q(\theta,z|\gamma,\phi))]-E_q[log(p(\theta, z |w,\alpha,\varphi))] \\
&=E_q[log(q(\theta,z|\gamma,\phi))]-E_q[log(p(\theta, z,w |\alpha,\varphi))]+log(p(w)) \\
&=-(E_q[log(p(\theta, z,w |\alpha,\varphi))]-E_q[log(q(\theta,z|\gamma,\phi))])+log(p(w)) \\
&=-\mathcal{L}(\gamma,\phi;\alpha,\varphi)+log(p(w))
\end {aligned}
$$
在上式中，令 $\mathcal{L}(\gamma,\phi;\alpha,\varphi)=E_q[log(p(\theta, z,w |\alpha,\varphi))]-E_q[log(q(\theta,z|\gamma,\phi))]$, 称为ELBO（Evidence Lower BOund）。
称其为ELBO是因为 $log(p(w))=\mathcal{L}(\gamma,\phi;\alpha,\varphi)+KL(q(\theta,z|\gamma,\phi)||p(\theta, z|w,\alpha,\varphi))\geq\mathcal{L}(\gamma,\phi;\alpha,\varphi)$。
根据上面的等式，$log(p(w))$是一个定值，因此要使 $KL(q(\theta,z|\gamma,\phi)||p(\theta, z|w,\alpha,\varphi))$最小，只要使得 $\mathcal{L}(\gamma,\phi;\alpha,\varphi)$最大即可。
之所以优化ELBO最大，是因为我们不知道隐变量的后验分布，无法直接优化KL散度最小。
下面计算ELBO。

推导$\mathcal{L}(\gamma,\phi;\alpha,\varphi)$

$$
\begin {aligned}
\mathcal{L}(\gamma,\phi;\alpha,\varphi)&=E_q[log(p(\theta, z,w |\alpha,\varphi))]-E_q[log(q(\theta,z|\gamma,\phi))] \\
&=E_q[log(p(\theta|\alpha))]+E_q[log(p(z|\theta))]+E_q[log(p(w|z,\varphi))]-E_q[log(q(\theta|\gamma))]-E_q[log(q(z|\phi))]
\end {aligned}
$$
下面分别推导这5项。

$E_q[log(p(\theta|\alpha))]$

$$
E_q[log(p(\theta|\alpha))]=\sum^{K}_{i=1}(\alpha_i-1)E_q[log\theta_i]+log\Gamma(\sum^{K}_{i=1}\alpha_i)-\sum^{K}_{i=1}log\Gamma(\alpha_i)
$$

$\theta$ is generated from $Dir(\theta|\gamma)$, 因此有$E_q[log\theta_i]=\psi(\gamma_i)-\psi(\sum^{K}_{j=1}\gamma_j)$, 因此：

$$
E_q[log(p(\theta|\alpha))]=\sum^{K}_{i=1}(\alpha_i-1)(\psi(\gamma_i)-\psi(\sum^{K}_{j=1}\gamma_j))+log\Gamma(\sum^{K}_{i=1}\alpha_i)-\sum^{K}_{i=1}log\Gamma(\alpha_i)
$$

$E_q[log(p(z|\theta))]$

$$
\begin {aligned}
E_q[log(p(z|\theta))]&=E_q[\sum^{N_d}_{n=1}\sum^{K}_{i=1}z_{ni}log\theta_i] \\
&=\sum^{N_d}_{n=1}\sum^{K}_{i=1}E_q[z_{ni}]E_q[log\theta_i] \\
&=\sum^{N_d}_{n=1}\sum^{K}_{i=1}\phi_{ni}(\psi(\gamma_i)-\psi(\sum^{K}_{j=1}\gamma_j))
\end {aligned}
$$
$\theta$ is generated from $Dir(\theta|\gamma)$ and $z$ is generated from $Mult(z|\phi)$。$N_d$表示第d个文档的单词总数。

$E_q[log(p(w|z,\varphi))]$

$$
\begin {aligned}
E_q[log(p(w|z,\varphi))]&=E_q[\sum^{N_d}_{n=1}\sum^{K}_{i=1}\sum^{M}_{j=1}z_{ni}w^{j}_{n}log\varphi_{ij}] \\
&=\sum^{N_d}_{n=1}\sum^{K}_{i=1}\sum^{M}_{j=1}E_q[z_{ni}]w^{j}_{n}log\varphi_{ij} \\
&=\sum^{N_d}_{n=1}\sum^{K}_{i=1}\sum^{M}_{j=1}\phi_{ni}w^{j}_{n}log\varphi_{ij}
\end {aligned}
$$

$E_q[log(q(\theta|\gamma))]$

$$
\begin {aligned}
E_q[log(q(\theta|\gamma))]&=\sum^{K}_{i=1}(\gamma_i-1)E_q[log\theta_i]+log\Gamma(\sum^{K}_{i=1}\gamma_i)-\sum^{K}_{i=1}log\Gamma(\gamma_i) \\
&= \sum^{K}_{i=1}(\gamma_i-1)(\psi(\gamma_i)-\psi(\sum^{K}_{j=1}\gamma_j))+log\Gamma(\sum^{K}_{i=1}\gamma_i)-\sum^{K}_{i=1}log\Gamma(\gamma_i)
\end {aligned}
$$

$E_q[log(q(z|\phi))]$

$$
\begin {aligned}
E_q[log(q(z|\phi))]&=E_q[\sum^{N_d}_{n=1}\sum^{K}_{i=1}z_{ni}log\phi_{ni}] \\
&=\sum^{N_d}_{n=1}\sum^{K}_{i=1}E_q[z_{ni}]log\phi_{ni} \\
&=\sum^{N_d}_{n=1}\sum^{K}_{i=1}\phi_{ni}log\phi_{ni}
\end {aligned}
$$

最终可以得到：
$$
\begin {aligned}
\mathcal{L}(\gamma,\phi;\alpha,\varphi)&=\sum^{K}_{i=1}(\alpha_i-1)(\psi(\gamma_i)-\psi(\sum^{K}_{j=1}\gamma_j))+log\Gamma(\sum^{K}_{i=1}\alpha_i)-\sum^{K}_{i=1}log\Gamma(\alpha_i) \\
&+\sum^{N_d}_{n=1}\sum^{K}_{i=1}\phi_{ni}(\psi(\gamma_i)-\psi(\sum^{K}_{j=1}\gamma_j)) \\
&+\sum^{N_d}_{n=1}\sum^{K}_{i=1}\sum^{M}_{j=1}\phi_{ni}w^{j}_{n}log\varphi_{ij} \\
&-(\sum^{K}_{i=1}(\gamma_i-1)(\psi(\gamma_i)-\psi(\sum^{K}_{j=1}\gamma_j))+log\Gamma(\sum^{K}_{i=1}\gamma_i)-\sum^{K}_{i=1}log\Gamma(\gamma_i)) \\
&-(\sum^{N_d}_{n=1}\sum^{K}_{i=1}\phi_{ni}log\phi_{ni})
\end {aligned}
$$

变分参数的更新

$\phi$的更新

$\mathcal{L}(\gamma,\phi;\alpha,\varphi)$式中包含$\phi$参数的项表示为：

$$
\mathcal{L}_{\phi_{ni}}=\phi_{ni}(\psi(\gamma_i)-\psi(\sum^{K}_{j=1}\gamma_j))+\phi_{ni}log\varphi_{iw}-\phi_{ni}log\phi_{ni}+\lambda(\sum^{K}_{j=1}\phi_{ni}-1)
$$
其中，$\phi_{ni}log\varphi_{iw}$项中的$w$表示该篇文档第$n$个词在词表中的编号，是对前面推导出的式子的等价变换。最后一项是为了使用拉格朗日乘子法加的一项，注意该项结果为0，目的是便于求导。

求导，得到：
$$
\frac{\partial{\mathcal{L}}}{\partial{\phi_{ni}}}=(\psi(\gamma_i)-\psi(\sum^{K}_{j=1}\gamma_j))+log\varphi_{iw}-log\phi_{ni}-1+\lambda
$$
令导数为0，得到：
$$
\phi_{ni}\propto\varphi_{iw}exp(\psi(\gamma_i)-\psi(\sum^{K}_{j=1}\gamma_j))
$$
因此可以根据该式计算$\phi$，再归一化即可。

$\gamma$的更新

$\mathcal{L}(\gamma,\phi;\alpha,\varphi)$式中包含$\gamma$参数的项表示为：

$$
\mathcal{L}_{\gamma}=\sum^{K}_{i=1}(\psi(\gamma_i)-\psi(\sum^{K}_{j=1}\gamma_j))(\alpha_i+\sum^{N_d}_{n=1}\phi_{ni}-\gamma_{i})-log\Gamma(\sum^{K}_{i=1}\gamma_i)+\sum^{K}_{i=1}log\Gamma(\gamma_i))
$$

求导，得到：
$$
\frac{\partial{\mathcal{L}}}{\partial{\gamma_{i}}}=\psi{‘}(\gamma_i)(\alpha_i+\sum^{N_d}_{n=1}\phi_{ni}-\gamma_i)-\psi{‘’}(\sum^{K}_{j=1}\gamma_{j})\sum^{K}_{j=1}(\alpha_j+\sum^{N_d}_{n=1}\phi_{nj}-\gamma_j)
$$

令导数为0，得到：
$$
\gamma_i=\alpha_i+\sum^{N_d}_{n=1}\phi_{ni}
$$
这样就得到了$\gamma$的更新公式。

变分推断算法流程

LDA的变分推断算法流程如下图，用来计算变分参数$\phi$和$\gamma$。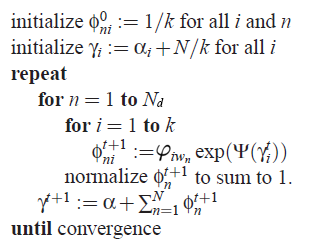
inference

Variational EM

变分EM算法流程

1.初始化充分统计量，根据充分统计量初始化模型参数$\alpha$和$\varphi$。
2.迭代执行以下步骤直到收敛：
(E-Step)对于每一篇文档，执行上述的变分推断算法，计算优化的变分参数$\phi$和$\gamma$，并根据变分参数计算充分统计量。
(M-Step)根据充分统计量，更新模型参数$\alpha$和$\varphi$。

M-Step

E-Step如何计算变分参数前面的变分推断算法已经介绍了，这里解释一下M-Step如何更新模型参数$\alpha$和$\varphi$。
同样是通过最大化ELBO来实现的。

$\varphi$的更新

$\mathcal{L}(\gamma,\phi;\alpha,\varphi)$式中包含$\varphi$参数的项表示为（对所有文档的值做了求和）,同样使用了拉格朗日乘子法：

$$
\mathcal{L}_{\varphi}=\sum^{N}_{d=1}\sum^{N_d}_{n=1}\sum^{K}_{i=1}\sum^{M}_{j=1}\phi_{dni}w^{j}_{dn}log\varphi_{ij}+\sum^{K}_{i=1}\lambda_{i}(\sum^{M}_{j=1}\varphi_{ij}-1)
$$
该式对 $\varphi_{ij}$求导并令导数等于0，可以得到:
$$
\varphi_{ij}\propto\sum^{N}_{d=1}\sum^{N_d}_{n=1}\phi_{dni}w^{j}_{dn}
$$

$\alpha$的更新

$\mathcal{L}(\gamma,\phi;\alpha,\varphi)$式中包含$\alpha$参数的项表示为:
$$
\mathcal{L}_{\alpha}=\sum^{N}_{d=1}(log\Gamma(\sum^{K}_{j=1}\alpha_j)-\sum^{K}_{i=1}log\Gamma(\alpha_i))+\sum^{K}_{i=1}((\alpha_i-1)(\psi(\gamma_{di})-\psi(\sum^{K}_{j=1}\gamma_{dj})))
$$
求导，得到：
$$
\frac{\partial{\mathcal{L}}}{\partial{\alpha_{i}}}=N(\psi(\sum^{K}_{j=1}\alpha_j)-\psi\alpha_i)+\sum^{N}_{d=1}(\psi(\gamma_{di}-\psi(\sum^{K}_{j=1}\gamma_{dj}))
$$
无法直接令导数等于0计算出$\alpha_i$。
计算出Hessian矩阵：
$$
\frac{\partial^{2}\mathcal{L}}{\partial{\alpha_{i}}\partial{\alpha_{j}}}=N(\psi{‘}(\sum^{K}_{j=1})-\delta(i,j)\psi{‘}(\alpha_i))
$$
使用牛顿法来优化$\alpha$。

LDA的实现

python实现的Variational EM LDA。用于训练和预测的数据集分别放在两个文本文件中，一行表示一篇文档，可处理中文和英文。
下面给出代码。本代码参考了David M.Blei的c语言源码。
变分推断以及EM的收敛条件可以通过计算likelihood来实现，这里设置了固定的循环次数。超参数alpha的更新被省略了，使用了初始值。
几个重要参数的对应关系见下表。

公式符号 代码符号 描述
$\alpha$ alpha 模型参数，document-topic分布的超参数
$\varphi$ varphi 模型参数，topic-word分布，代码中取了对数
$\gamma$ gamma 变分参数，当前推断文档的topic分布
$\phi$ phi 变分参数，当前推断文档的每个词语的topic分布

本代码先用训练数据训练得到一个模型，输出了得到的每个topic的top10的词语，然后对新来的测试文档进行了推断，通过$\gamma$参数得到预测的该文档属于的主题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
import numpy as np
import codecs
import jieba
import re
import random
import math
from scipy.special import psi

# itemIdList : the list of distinct terms in the document
# itemCountList : the list of number of the existence of corresponding terms
# wordCount : the number of total words (not terms)
class Document:
    def __init__(self, itemIdList, itemCountList, wordCount):
        self.itemIdList = itemIdList
        self.itemCountList = itemCountList
        self.wordCount = wordCount

# preprocessing (segmentation, stopwords filtering, represent documents as objects of class Document)
def preprocessing():
    
    # read the list of stopwords
    file = codecs.open('stopwords.dic','r','utf-8')
    stopwords = [line.strip() for line in file]
    file.close()
    
    # read the corpus for training
    file = codecs.open('dataset.txt','r','utf-8')
    documents = [document.strip() for document in file] 
    file.close()
    
    docs = []
    word2id = {}
    id2word = {}
    
    currentWordId = 0
    for document in documents:
        word2Count = {}
        # segmentation
        segList = jieba.cut(document)
        for word in segList: 
            word = word.lower().strip()
            # filter the stopwords
            if len(word) > 1 and not re.search('[0-9]', word) and word not in stopwords:
                if word not in word2id:
                    word2id[word] = currentWordId
                    id2word[currentWordId] = word
                    currentWordId += 1
                if word in word2Count:
                    word2Count[word] += 1
                else:
                    word2Count[word] = 1
        itemIdList = []
        itemCountList = []
        wordCount = 0

        for word in word2Count.keys():
            itemIdList.append(word2id[word])
            itemCountList.append(word2Count[word])
            wordCount += word2Count[word]

        docs.append(Document(itemIdList, itemCountList, wordCount))

    return docs, word2id, id2word
    
def maxItemNum():
    num = 0
    for d in range(0, N):
        if len(docs[d].itemIdList) > num:
            num = len(docs[d].itemIdList)
    return num

def initialLdaModel():
    for z in range(0, K):
        for w in range(0, M):
            nzw[z, w] += 1.0/M + random.random()
            nz[z] += nzw[z, w]
    updateVarphi()    

# update model parameters : varphi (the update of alpha is ommited)
def updateVarphi():
    for z in range(0, K):
        for w in range(0, M):
            if(nzw[z, w] > 0):
                varphi[z, w] = math.log(nzw[z, w]) - math.log(nz[z])
            else:
                varphi[z, w] = -100

# update variational parameters : gamma and phi
def variationalInference(docs, d, gamma, phi):
    phisum = 0
    oldphi = np.zeros([K])
    digamma_gamma = np.zeros([K])
    
    for z in range(0, K):
        gamma[d][z] = alpha + docs[d].wordCount * 1.0 / K
        digamma_gamma[z] = psi(gamma[d][z])
        for w in range(0, len(docs[d].itemIdList)):
            phi[w, z] = 1.0 / K

    for iteration in range(0, iterInference):
        for w in range(0, len(docs[d].itemIdList)):
            phisum = 0
            for z in range(0, K):
                oldphi[z] = phi[w, z]
                phi[w, z] = digamma_gamma[z] + varphi[z, docs[d].itemIdList[w]]
                if z > 0:
                    phisum = math.log(math.exp(phisum) + math.exp(phi[w, z]))
                else:
                    phisum = phi[w, z]
            for z in range(0, K):
                phi[w, z] = math.exp(phi[w, z] - phisum)
                gamma[d][z] =  gamma[d][z] + docs[d].itemCountList[w] * (phi[w, z] - oldphi[z])
                digamma_gamma[z] = psi(gamma[d][z])


# calculate the gamma parameter of new document
def inferTopicOfNewDocument():
    testDocs = []
    # read the corpus to be inferred
    file = codecs.open('infer.txt','r','utf-8')
    testDocuments = [document.strip() for document in file] 
    file.close()
    
    for d in range(0, len(testDocuments)):
        document = testDocuments[d]
        word2Count = {}
        # segmentation
        segList = jieba.cut(document)
        for word in segList: 
            word = word.lower().strip()
            if word in word2id:
                if word in word2Count:
                    word2Count[word] += 1
                else:
                    word2Count[word] = 1
                      
        itemIdList = []
        itemCountList = []
        wordCount = 0

        for word in word2Count.keys():
            itemIdList.append(word2id[word])
            itemCountList.append(word2Count[word])
            wordCount += word2Count[word]

        testDocs.append(Document(itemIdList, itemCountList, wordCount))
    
    gamma = np.zeros([len(testDocuments), K])
    for d in range(0, len(testDocs)):
        phi = np.zeros([len(testDocs[d].itemIdList), K])
        variationalInference(testDocs, d, gamma, phi)
        
    return gamma
           
docs, word2id, id2word = preprocessing() 

    
# number of documents for training
N = len(docs)
# number of distinct terms
M = len(word2id)
# number of topic
K = 10
# iteration times of variational inference, judgment of the convergence by calculating likelihood is ommited
iterInference = 20 
# iteration times of variational EM algorithm, judgment of the convergence by calculating likelihood is ommited
iterEM = 20

# initial value of hyperparameter alpha
alpha = 5
# sufficient statistic of alpha
alphaSS = 0
# the topic-word distribution (beta in D. Blei's paper)
varphi = np.zeros([K, M])
# topic-word count, this is a sufficient statistic to calculate varphi
nzw = np.zeros([K, M])
# topic count, sum of nzw with w ranging from [0, M-1], for calculating varphi
nz = np.zeros([K])

# inference parameter gamma
gamma = np.zeros([N, K])
# inference parameter phi
phi = np.zeros([maxItemNum(), K])

# initialization of the model parameter varphi, the update of alpha is ommited
initialLdaModel()

# variational EM Algorithm
for iteration in range(0, iterEM): 
    nz = np.zeros([K])
    nzw = np.zeros([K, M])
    alphaSS = 0
    # EStep
    for d in range(0, N):
        variationalInference(docs, d, gamma, phi)
        gammaSum = 0
        for z in range(0, K):
            gammaSum += gamma[d, z]
            alphaSS += psi(gamma[d, z])
        alphaSS -= K * psi(gammaSum)

        for w in range(0, len(docs[d].itemIdList)):
            for z in range(0, K):
                nzw[z][docs[d].itemIdList[w]] += docs[d].itemCountList[w] * phi[w, z]
                nz[z] += docs[d].itemCountList[w] * phi[w, z]

    # MStep
    updateVarphi()

# calculate the top 10 terms of each topic
topicwords = []
maxTopicWordsNum = 10
for z in range(0, K):
	ids = varphi[z, :].argsort()
	topicword = []
	for j in ids:
		topicword.insert(0, id2word[j])
	topicwords.append(topicword[0 : min(10, len(topicword))])

# infer the topic of each new document
inferGamma = inferTopicOfNewDocument()
inferZ = []
for i in range(0, len(inferGamma)):
    inferZ.append(inferGamma[i, :].argmax())

实验结果

继续沿用了前面用过的数据集。

English

英文数据集采用关于one piece的16个英文文档，来源于维基百科。
设置的参数为K=10，iterInference=20，iterEM=20。
实验结果如下图。给出了每个主题top10的词语。
topics
此外用于预测的两个文档见下图，这两句话不在训练集之中，是新写的两句话，分别被预测为了主题7和主题2，对比上面的图可以看出预测的十分正确。
predict
当然，如果需要预测主题的文档中的大多数词都没在训练集中出现过，比如你用英文文档来训练，用中文文档来预测，那么预测的结果肯定是不对的。

Chinese

中文数据集采用5000篇新浪社会新闻。
设置的参数为K=30，iterInference=20，iterEM=20。
实验结果如下图。给出了每个主题top10的词语。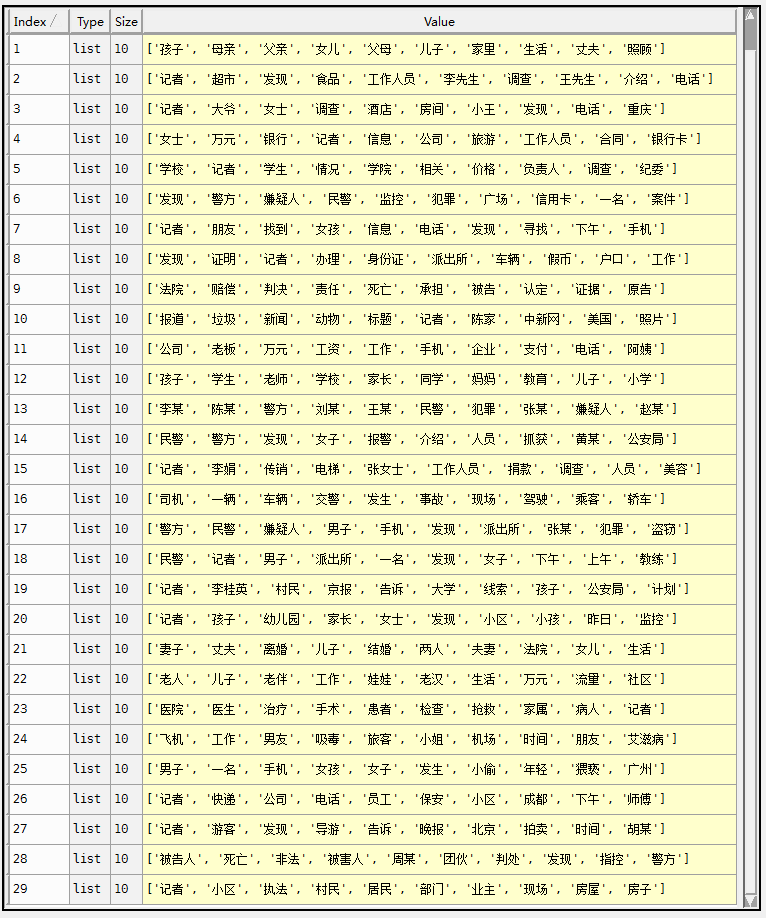
topics2
此外用于预测的两个文档见下图，这两个新闻不在训练集之中，是另外的两条新闻，分别被预测为了主题25和主题9。
predict2

参考资料

1 Latent Dirichlet Allocation by David M. Blei et al.
2 Variational Inference by David M. Blei
3 Variational Inference for LDA by Zhao Zhou

完整代码、停用词以及数据集已托管至 github